MORSYS
Binary Simplex, Inc. was awarded a patent titled "Spatial Decomposition Methods Using Bit Manipulation," on August 17, 2010. It is our aim to continue to develop this product and to arrange narrow-spectrum licensing agreements with various industries interested in using our processes.
Strengths and Advantages
The way the Morsys algorithm deconstructs and manipulates volumetric data delivers several advantages over existing methods of processing and viewing volumetric data. This section describes these strengths and advantages at a fairly high level.
Neighbor-Finding
At the root of the algorithm is its ability to find neighboring shapes in a volumetric data set and to deconstruct it on the fly into a regular tetrahedral mesh by using bit manipulation instead of one of the traditional methods, which use parent-child relationships to form “tree” structures that must be held in the computer’s memory (either RAM or hard drive). This neighbor-finding ability allows the hyper-efficient manipulation of volumetric data and provides the foundation for all of the advantages detailed in the following sections.
Processing Efficiency
The Morsys algorithm’s ability to handle volumetric data much more efficiently than current methods, allows current problems requiring real-time solutions to be solved using fewer processor cycles resulting in less hardware investment. The reduced hardware requirements also allows current hardware to tackle more complex problems in significantly reduced time frames, including moving significantly more complex data processing tasks to mobile computing platforms.
Most current volumetric data manipulation methods involve building a huge directory of parent-child relationships in a hierarchical tree-type structure, holding as much of that information in RAM as possible and reverting to hard drive storage when RAM is insufficient to the size of the data set. The entire data set must be decomposed to whatever final level of detail is desired, and then must be stored in this structure prior to any viewing or manipulation. When a surface of an image is viewed, the entire data set must be evaluated in order to produce the image and must be re-evaluated each time the view is altered (e.g., repositioning or zooming).
Lower Memory Use
With the Morsys algorithm, no pre-decomposition must be done. The algorithm’s ability to decompose a data set on the fly to variable levels of detail as required for the current view, has several benefits (see the “Constant Time” and “Progressive Rendering” sections below), but one of them is that much less memory is needed to view and manipulate the image. It is important to note that when we say that the data set only needs to be decomposed “to variable levels of detail as required for the current view,” we really mean that only the currently viewed portion of the image matters. The Morsys algorithm is capable of handling different parts of a data set at different resolutions, something that current volumetric data manipulation methods cannot do.
This means that when working with a data set—for example, an MRI of a full human body and viewing a high-res image of the surface of the pancreas—the surface is rendered to whatever level of detail required using millions of regular tetrahedra, but the parts of the data set that are not currently being used are only deconstructed to a crude level of detail and only a few hundred or thousand tetrahedra are used for the entire rest of the body. If the user chooses to move to another view, say she wishes to view the obverse of the pancreas, the algorithm reduces the resolution of the unneeded side of the pancreas and decomposes the new view to whatever level of detail the user needs, up to the maximum resolution of the MRI scan.
Current image manipulation methods would require the entire body-image data set to be decomposed to whatever level of detail the user needed, even if she was only viewing a small part of the image. This would have resulted in billions of data points needing to be calculated and processed in order to view only a tiny fraction of them, and all of those data points would need to be recalculated each time the user wished to change her viewpoint. Currently, this is accomplished by chopping larger data sets into smaller ones that are more easily processed or, if real-time viewing is required, by throwing massively parallel hardware at the problem. If real-time data manipulation is not required, more modest hardware configurations can be used up to the point where processing time exceeds the time the user finds acceptable.
Constant Time
As described above, the Morsys algorithm does not require the volumetric data set to be deconstructed into a hierarchical tree-type structure. Current volumetric data manipulation methods use these tree structures to identify the nearest common ancestors between data points when trying to work with the data in their attempts to solve the problem of identifying their neighbors. Due to the nature of this decomposition method, the memory needed to store and the processor cycles needed to manipulate a data set increase more quickly than the actual size of the data set.
Take for example an exceedingly small data set with only two data points. To deconstruct this data set into the hierarchical tree structure, three data points are needed: the two data points from the data set and their single common ancestor. So the resulting structure has one parent and two child data points, and the nearest common ancestor of each child is only one level away, so finding the neighboring data point on the bottom of the structure is a simple exercise.
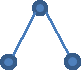
Figure 1 : A 2-Point Data set in a Hierarchical Structure
If this data set were to increase by one, to three data points, a constant-time result would be for the resulting structure to have only four data points. But, as is shown in the figure below, a three-point data set may take five or even six points to represent all the parent-child relationship in a hierarchical tree. The problem of finding neighbors in this data set is significantly more complex since the nearest common ancestor could be one or two levels up the tree.
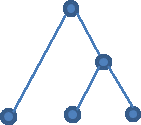
Figure 2 : A 3-Point Data set in a Hierarchical Structure
In the final example, a volumetric data set with six points is shown using eleven data points to build the hierarchical structure. So the six-point data set, while only 100% larger than the three-point, takes 120% more storage space and processor cycles to manipulate. And the problem of finding neighbors becomes even more complex, requiring between two and five steps.
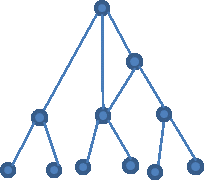
Figure 3 : A 6-Point Data set in a Hierarchical Structure
The Morsys algorithm is a constant-time (as opposed to exponential-time, logarithmic-time, or some other greater than 1:1-time) solution to storing and manipulating volumetric data, which means that a data set that is 100% larger than another, will take 100% more storage space and up to 100% more processor cycles to manipulate. And the problem of finding neighbor tetrahedral is always as simple as flipping a single binary bit in the tetrahedron’s location code; a process which computers are essentially built for and is hyper efficient.
In the previous section, we highlighted that the Morsys algorithm can handle various parts of a data set at different resolutions, so in most cases the processor cycles to compute a volumetric data set will be far fewer than those needed to process the same data set using current methods. Thus, the efficiency gains from using this technology go far beyond the benefits from its constant-time abilities but the constant-time functions contribute to its overall superiority to any other volumetric data manipulation method currently in use.
Progressive Rendering
In the previous sections, we’ve touched on the ability of the Morsys algorithm to decompose a data set to whatever level of resolution is needed and to further resolve the data as needed. This ability to progressively render a data set has two major advantages compared to current methods, which only allow an image to be viewed once the entire data set has been rendered to whatever level of detail is required.
Quick Adjustments to a View With Lo-Res Data
Often when a user is viewing surfaces from a volumetric data set, she needs to make several adjustments to the view as she zeros in on an area of interest. Using the MRI example again, the user may be looking for an overly dense section of tissue in a lung but is working from a full-body scan. The progressive-rendering ability of the Morsys algorithm will allow her to look at a very rough view of the full body and will progressively refine the image until the user tells the software to stop or change the view. The progressive rendering is a smooth process where the viewer sees the full image at increasing levels of detail, without “tearing” or “cracking” artifacts which are common when viewing an data set at less than maximum resolution with current methods.
Instead of waiting for a full-resolution image of the body to load and then selecting the chest area to view (with another wait time as the current methods recalculates the entire data set, even though only a subset is now being used), the user will be able to quickly see a general shape of the body rendered with only a few hundred or thousand tetrahedra and direct the software to zoom to the desired area, repeating as needed until the area of interest is displayed on the screen. The final image can then be progressively rendered with finer and finer levels of detail as the software continues to make passes over the data set to refine the displayed surface.
Pushing Successively Resolved Data Over a Network
When working over a network, whether because a hospital’s server room is a few hundred feet away, or because the user is a telehealth specialist who is in San Francisco and is manipulating an MRI data set that is stored on a server in northern Alaska, the ability to see the image at a low resolution and make adjustments prior to waiting for a full download and processing, is a true time-saver.
As the use of electronic health record systems continue to expand into medical facilities, and as practitioners are more and more likely to carry mobile devices to access those systems wirelessly, the progressive-rendering feature of the Morsys algorithm becomes more important due to the lower bandwidth nature of wireless connections and the lower processing capacity of mobile computing platforms such as tablets and smartphones.
Improved Collision Detection
One of the essential criteria of computer gaming, military and other simulators, and certain other applications is for the computer to “know” when two onscreen objects collide. This detection system allows objects in the game or simulation to interact with each other. Using World of Warcraft as an example, collision detection is what stops a user character, a “toon,” from walking through a building’s wall because the servers detect that the toon has collided with a wall and does not allow the toon to continue its forward movement. Determining whether a toon’s feet are touching (colliding with) the ground is what decides whether the toon should fall; and if the toon falls, collision detection is what determines when the toon reaches the ground and the fall should suddenly be arrested. Collision detection determines whether a toon’s sword has collided with a monster’s head, so the system knows that if the monster has been killed and the toon should be awarded some experience points.
While these collision-detection processes have been improving significantly as hardware has improved, they still use some degree of approximation, a higher degree in PC-based games where computing power is relatively low, and a lower degree in, say, military simulations when massively parallel hardware can be thrown at the problem and where there is a need for the simulations to behave as realistically as possible.
As a simplified overview, current collision detection is handled by drawing invisible “frames” around objects to define the objects’ boundaries. As all data in a game or simulation must be considered, whether or not it’s viewable by the player, these frames are almost always less complex than the object they’re bounding, except in cases where they exactly match very simple objects. The more complex a shape, the less the collision frame will conform to its actual contours. As mentioned above, collision detection has greatly improved as the power of computer processors has improved over the years. The figure below shows a basic example of how a simple four-sided collision frame would have misinterpreted the collision state of two onscreen sprites, and a 50% more complex six-sided frame would have correctly interpreted the collision state.
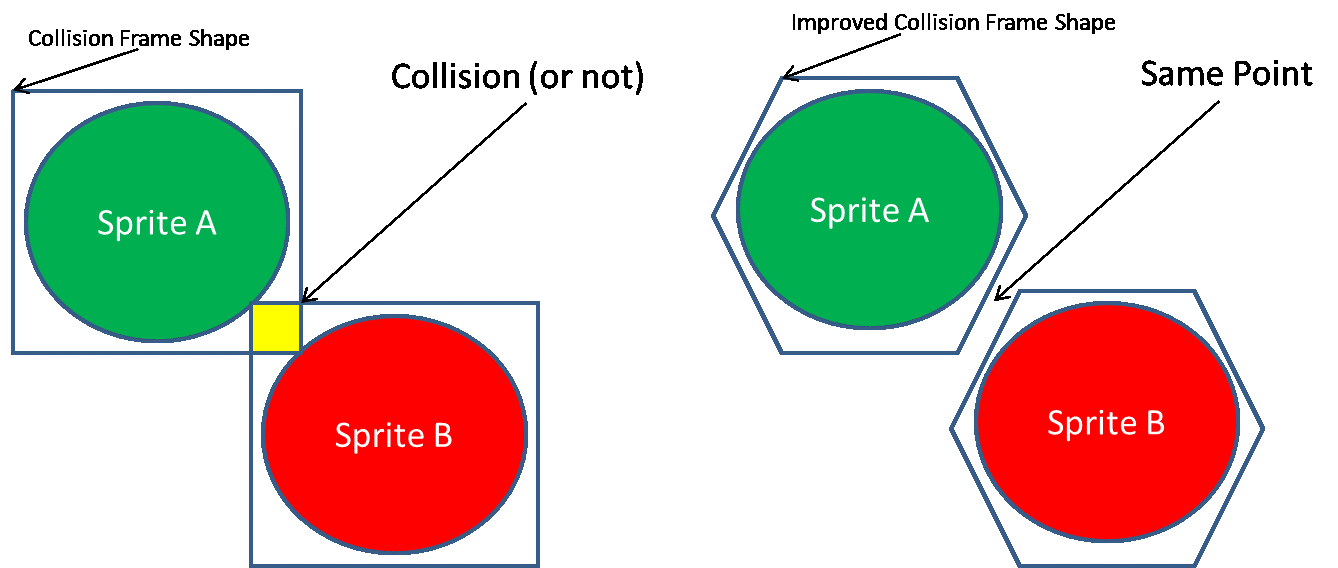
Figure 4 : Basic Collision Detection
With the increase in processing power and the ability to doing more complex calculations, collision-detection frames have continued to evolve to allow better and better approximations. But “better” approximation is still approximation. Given the neighbor-finding abilities of the Morsys algorithm, approximation for collision detection is no longer needed. When volumetric data is used, the object itself will be its own collision-detection frame, and regardless of how organic the object is, there will be a 1:1 correlation between its shape and its collision-detection boundaries. PC games, providing they’re using volumetric data, will be able to have the same collision-detection precision as is found in the most hardcore military or surgical simulators. Granted, a PC game will be dealing with more simple data sets because the PC won’t have the processing power of the vastly more expensive simulator systems, but the disparity in collision-detection precision between the two systems will have been eliminated.
Avoiding Discontinuities
The previous section explained how the Morsys algorithm eliminated the need for using collision-detection frames as proxies for actual shapes, but traditional methods of volumetric data manipulation also use approximation when displaying an image at any resolution lower than its maximum level of detail. As processing power and data-manipulation techniques have improved, these approximations have been refined and reduced to the point where there impact is often unnoticeable to the human eye. However, the word often has to remain in that sentence. In entertainment applications such as computer gaming, a little bit of approximation in the data won’t cause any actual harm. Even if the approximation was significant enough to cause an artifact in the display that was noticeable to the human eye and caused a diminished user experience, no real harm would result.
There are areas where even minuscule approximations can cause unwanted or even harmful outcomes. An example is weather or ocean-current modeling, where the tiniest early flaw in the model can effect significant change downstream (the digital butterfly flapping its wings in China causing a digital hurricane in the Caribbean six months later). Another area negatively impacted by any amount of approximation is medical imaging, particularly as it relates to clinical decision support (CDS). Computer systems are more frequently being asked to support clinical practice by evaluating large amounts of data. A largely untapped field, which is described in greater detail later in this document, is CDS through evaluation of volumetric medical imaging data.
Combining the neighbor-finding and nonapproximation advantages of the Morsys algorithm, CDS systems can be trained to sift through large numbers of scans, comparing results to expectations looking for tumors, bone density or formation problems, weak blood vessel walls, dental caries or malformations, and a host of other medical issues, far more quickly than any human could. It may be able to identify potential issues when they have not yet progressed to a point where a human would notice them in a scan, or to evaluate areas of data sets on which humans haven’t had the time to focus.
Using a data-deconstruction system that allows for cohesive images at various levels of detail without cracking or tearing, will reduce both false positives and false negatives resulting from these CDS services. Reducing false positives lowers medical costs and patient stress, while reducing false negatives can improve patient outcomes and lower liability.
Technology Limitation
The Morsys algorithm is primarily applicable to volumetric data and is not as valuable when used with 2D data. For example, the current DICOM medical imaging data standard stores images as slices, not as truly volumetric data. The Morsys algorithm can be used to analyze data in the 2D format, but the benefits are much greater if the DICOM files are translated back into truly volumetric forms.
